Tau: you spin me right round
- Mark Huber

- Feb 11, 2019
- 2 min read
Okay, so there still seems to be some confusion about Tau versus Pi. Tau is the full circle constant, and represents 360 degrees, so one rotation around a circle. Pi is the half circle constant, and represents 180 degrees, one half of a rotation around a circle. So writing your angle as 3*Pi is about the same as saying ''I walked three half-miles'' rather than ''I walked 1.5 miles.''
Everyone I know does not describe distances in half miles, but still most mathematicians I know describe things in terms of half-rotations around a circle. I know everyone has been raised to use Pi, all our textbooks and exam questions are written with Pi, and change hurts. That being said, in this case the change is worth it!
For one thing, the labeling of Pi as the half circle constant and Tau as the full circle constant immediately makes their relationship clear, and I would argue makes what Pi is more clear to students as well.
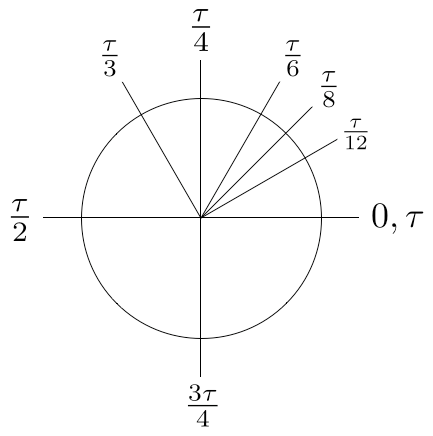
As a side benefit, the unit circle appears much nicer when using Tau. For instance, (3/4)Tau is actually three-fourths of the way around the circle, there is no need to mentally convert to half rotations.
I was reminded of this when a student asked if Wolfram Alpha could handle the constant tau. Sadly it does not. Here's a screen shot of what happens.
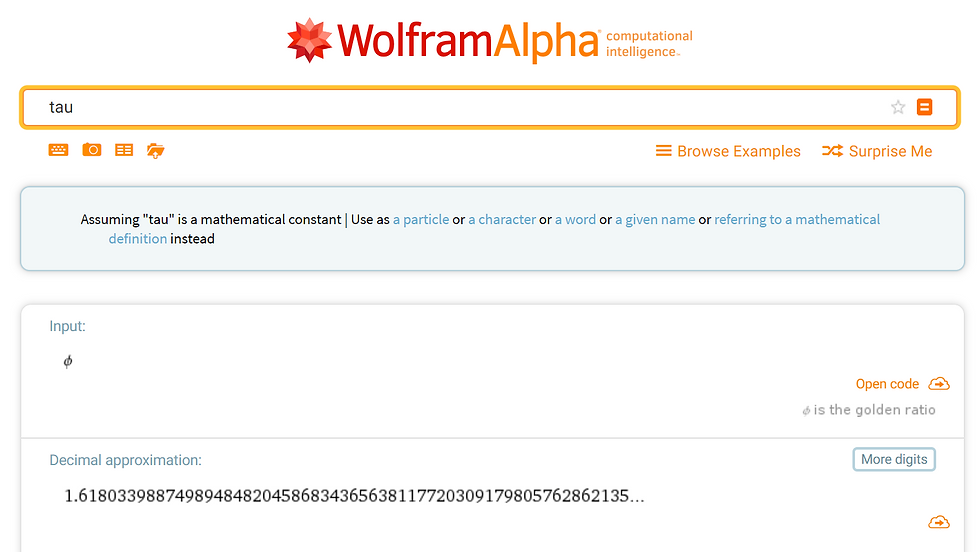
Wow! Not only does WolframAlpha not know what Tau is, it mistakes it for Phi!
To see if anyone else had this same issue, I did a Google search, while turned up this Wolfram blog entry studying the use of Pi versus Tau. The calculations that Mathematica can do are really quite amazing. In this case they used Mathematica formuals on mathematics papers in the arXiv that had been converted to .xhtml to see how many formulas that used Pi would have been simpler if Tau had been used instead.
Unfortunately, this kind of misses the point, and is part of a larger mistake about mathematics. High schools do their utmost to convince students that mathematics is all about manipulating formulas, but that is not really what math is all about. Mathematics is about finding patterns where the same idea can be used multiple times to get results across disciplines.
How does that relate to Tau versus Pi? Well, mathematician like to use integers. It makes our lives easier not to introduce unneeded complexity. But in the case of Pi, we are not measuring integers winds around the circle, but half winds around the circle. Most of the most famous formulas involving Pi (such as the density of a normal distribution or the period of the sine function) must have a 2Pi in them. In others, it just makes things more difficult to memorize. For instance, the area of a slice of a circle is (1/2)Theta r^2, where Theta is the angle. That makes the area of the whole circle (1/2)Tau r^2, but by using Pi instead ends up canceling the 2 and making the formulas look different from each other when they are really the same. The formula Pi r^2 might look superficially simpler than (1/2)Tau r^2, but when you think about it as a special case of (1/2)Theta r^2, something has been lost.
























Comments